[7][8][10]
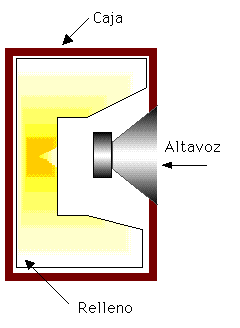
Para el diseño de un altavoz en caja cerrada ( fig VII.15) se representa la carga acústica de la caja tal como se observa en la figura VII.16, la cuál es una simplificación de la figura VII.12 eliminando la porción del ducto y despreciando las pérdidas de la caja .
Combinando los elementos en serie podemos obtener el modelo simplificado de la figura VII.17 y reflejando el sistema al lado eléctrico del modelo tenemos el circuito de la figura VII.18 .
Los parámetros de los circuitos anteriores son
Elasticidad acústica total del sistema:
(VII.26)Resistencia acústica total del sistema:
(VII.27)además:
(VII.28)
(VII.29)
(VII.30)
El circuito presentado es únicamente válido para el rango de frecuencias en donde el altavoz se comporta como un pistón, estas frecuencias deben corresponder a longitudes de onda tales que l/16>l donde l es la longitud efectiva de un ducto cerrado del mismo diámetro del altavoz y de volumen igual a la caja cerrada.
Los valores de los elementos del circuito se asumen que son independientes de la frecuencia en este rango. Los efectos de la inductancia de la bobina y la resistencia de la carga de radiación son despreciables.
La función de la respuesta del sistema de caja cerrada G(s) se puede obtener fácilmente del circuito de la figura VII.16, así como también la función de desplazamiento de la bobina X(s); la función de la impedancia de la bobina ZVC(s) se obtiene del circuito de la figura VII.18
A continuación se definen cada una de las funciones
La respuesta del sistema es:
(VII.31)La función del desplazamiento del cono viene dada por:
(VII.32)La función de la impedancia eléctrica del sistema es:
(VII.33)En donde cada uno de los parámetros son:
wc =2¹fc frecuencia de resonancia del sistema, dado por
(VII.34)QMC Factor Q del sistema a fC considerando únicamente las resistencias no eléctricas, dado por
(VII.35)QEC Factor Q del sistema a fC considerando solo la resistencia eléctrica RE , dado por
(VII.36)QTCO Factor Q total del sistema a fC cuando la resistencia de salida de la fuente RG=0, dado por
(VII.37)QTC Factor Q total del sistema a fC incluyendo todas las resistencias del sistema, dado por
(VII.38)a : Relación de elasticidad del sistema, dado por
(VII.39)
La función de respuesta en frecuencia de un sistema de caja cerrada se corresponde con un filtro pasa alto de segundo orden (pendiente de la banda de corte de 12 dB /octava). Esta función contiene la información a baja frecuencia de: la amplitud, la fase, el retardo y las características de la respuesta transiente de los sistemas de caja cerrada.
En la figura VII.19 se pueden apreciar las distintas curvas correspondientes a la amplitud de la respuesta en frecuencia normalizada de caja cerrada para distintos valores de QTC.
La eficiencia del sistema de caja cerrada en la región pasante, también llamada eficiencia de referencia de sistema, es la que se obtiene operando con un valor particular de carga de masa de aire dada por la caja, definida por
(VII.40)donde
(VII.41)Es un volumen que tiene la misma elasticidad acústica total de la suspensión del altavoz y del aire encerrado en la caja actuando juntos.
La ecuación anterior puede ser reescrita como
(VII.42)donde:
f3 Frecuencia de corte (media potencia o -3 dB) del sistema
VB Volumen interno neto de la caja del sistema
kn Constante de eficiencia del sistema dada por
(VII.43)La ecuación VII.43 muestra claramente la relación entre la eficiencia, el ancho de banda y el volumen de la caja del sistema. La máxima eficiencia posible para un sistema de caja cerrada viene dada por
(VII.44)donde f3 está en Hz y VB está en m3.
La potencia acústica del sistema está limitada por el desplazamiento de la bobina. Suponiendo un desplazamiento lineal del diafragma, la potencia acústica viene dada por
(VII.45)Donde VD es el volumen del desplazamiento pico del diafragma del altavoz
(VII.46)La ecuación de potencia acústica se puede reescribir como
(VII.47)donde kp es una constante de relación de potencia dada por
(VII.48)
El máximo valor de kp ocurre para un QTC cuyo valor este cercano a 1.1, en este caso la potencia máxima de los sistemas de caja cerrada viene dada por
(VII.49)
Luego, para diseñar una caja acústica cerrada a partir de los parámetros de Thiele y Small se debe seguir el siguiente procedimiento:
1.- Se selecciona el QTC a partir del tipo de respuesta deseada (figura VII.19.).
2.- Dependiendo de relleno o no de la caja tendremos
(VII.50)
donde:
Q'TC= QTC ajustando tomando en cuenta pérdidas
QA= 5 para cajas con relleno y 10 para cajas sin relleno
3.- Se calcula la relación a:
(VII.51)
4.- Se calcula el volumen de la caja VB:
(VII.52)
(VII.53)
donde :
Caja sin relleno:
Caja con relleno:
5.- La frecuencia de resonancia de la caja será:
(VII.54)
6,- Se grafica la respuesta del sistema:
(VII.55)
donde:
